Details
Note that this is my best assessment of what's going on with the glazier's bench, based on some but not exaustive study. If anyone finds anything wrong with this, please provide me with data and I'll do my best to correct -- CuriouserRandy.
Response to Single Charcoal Addition
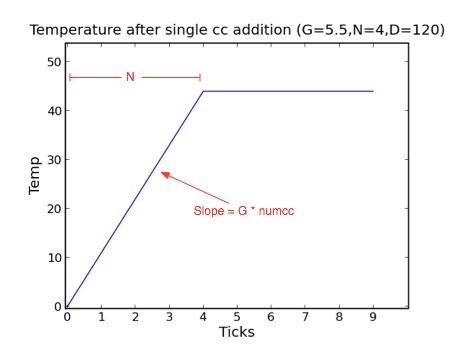
When charcoal is added to a glazier's bench, the result is an "impulse function" of some number of ticks of temperature rising, followed by some number of it holding steady. An impulse function is completely described by two numbers:
- The slope of the initial rise (temperature/tick). This is proportional to the amount of charcoal added; that proportionality constant (referred to as "G" for growth phase) is fixed for a particular bench.
- The length of the initial rise (number of ticks; referred to as "N"). This is fixed for a particular bench.
Graphically this looks like:
When no impulse function is active, the temperature at a bench falls by a constant amount each tick (referred to as "D" for dropping). A bench is completely specified by values for G, N, and D.
Response to two (or more) impulses
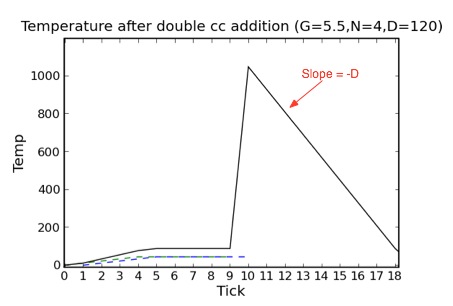
Two impulse functions sum linearly while both are active. I.e. if two charcoal is added on each of two successive ticks, the result will be (assuming N=4, G=5.5):
- 0 (two charcoal added)
- 11 (first impulse growing; two more charcoal added)
- 33 (both impulse growing)
- 55 (both impulse growing)
- 77 (both impulse growing)
- 88 (only second impulse growing)
- 88 (both impulses in steady state)
When the first impulse ends (nine ticks after it started), if there is a second impulse active there will be a spike. The size of this spike will be equal to the number of ticks for which both impulses were active times D. (My rationalization for this is that an impulse function is both raising temperature and preventing the temperature drop that would occur if there were no impulse function; the second impulse function has nothing to do with this second action, and so stores it up until the first impulse function is done and lets it all out at once :-}). Graphically, this looks like:
(The linear summation described above can been seen in a close up of this picture:
If two impulses have identical spans (e.g. you added 2 cc twice in the same tick) they just add linearly; no spike occurs.
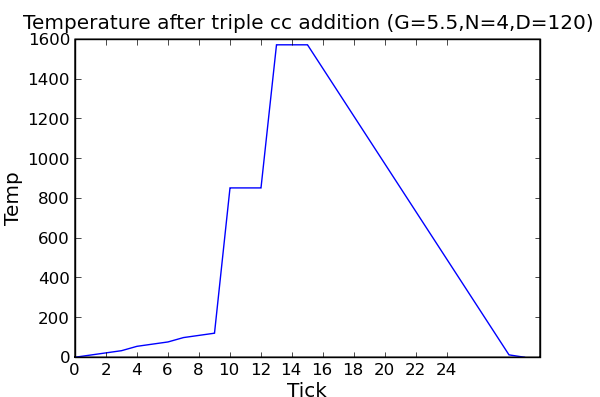
Note that more than two impulse functions are resolved in order. I.e. the second one added causes a spike when the first one ends, and the third one added causes a spike when the second one ends. I.e.
Calibration
If you trust this theory (:-}), you can calibrate a bench by adding 2 cc, waiting two ticks, and adding two more cc. The temperature response should look like
(0, 2G, 4G, 8G, 12G, ... (growing to) ..., 4 * N * G, ... (holding steady until) ..., 4 * N * G + 7 * D)
At that point it will hold steady for two ticks, and then drop by D per tick. This will give you all three numbers.
If you don't trust this theory (which is my usual mode), I'd recommend adding 2cc three times with four ticks between each addition. This will let you see each tick, verify the 9 tick total length (the spikes will occur at tick 10 and 14 if so), and give you multiple reads on all of G, N, and D. Figuring out what this curve should look like is more complicated, as you'll have growth times and spikes adding depending on the value of N.
Practical Notes
- Tick time is approximately ten seconds plus server lag (this is the point in this document I'm least certain of). This means that the total time during which temperature will rise or stay constant after a cc addition is ~90 seconds.
- The spike will in general occur about a minute and a half after your first charcoal addition. Don't get impatient and add more cc, or you'll be waiting a while for the temperature to come back down and possibly cursing product loss.
- For a single charcoal addition, the total temperature increase will be N * G * numcc.
- For a second, overlapping charcoal addition the total temperature increase is N * G * (numcc1 + numcc2) + overlap * D.
- Note that because of the latter you can drop the spike size, making "spiking" a possible technique for moving within the 1600-2400 band. The smallest total temperature increase easily acheivable (because you can tell when the ticks are) is 4 * N * G + (9-N) * D. If this is less than 800 (which it usually is) you can manage your bench temperature by adding 2cc whenever it begins to drop until it's near 1600 (a single impulse will gain you 2 * N * G and waiting for the drop will lose you D; usually D is greater than 2 * N * G, so you'll drop temperature down through the range gradually over time). At that point you can do a mimimal spike by adding 2 cc, waiting N ticks, and adding another 2 cc, at which point you're at the top of the range again. Among other things, this technique is very charcoal efficient; you can run your bench only adding 2cc increments about every 90 seconds.
- You can predict exactly what the temperature should be for your next charcoal addition for each bench. This means that you don't need to catch when the temperature changes, only when it hits a given value. This makes running multiple benches much easier.
- My python generator functions are attached below; use at your own risk.