Overview
The Pyrotechnics technology is available at Universities of Art and Music. This skill allows players to create displays of fireworks with stars made in a Star Rack that are then loaded into a Fireworks Mortar. A multitude of patterns and arrays can be achieved for fun or for the The Test Of Pyrotechnics. Also see Pyrotechnics Contest Schedule, Pyrotechnics Stadium Locations and Pyrotechnics Examples.Star formulas can be gained at Universities of Art and Music. Additional stars may be made available by experimentation with a Portable Star Lab (see page for details), which must then be returned to a University. 2 star formulas are available at all universities with Pyrotechnics opened; currently 5 more are only available at Karnak, 2 more at Sanai, 1 more at Lower Nubia, 21 at Pharaohs Bay and 3 more at Valley of Kings. See the Star Rack page for the formulas.
The remainder of this page covers the use and design of fireworks.
Quick reference
See Also:
- Pyrotechnics Stadium Locations - where to go when the going stars glowing.
- Pyrotechnics Contest Schedule - what people have planned (don't be shy to add your own!)
- Star rack - also for what various stars look like
- KaBoom Pyrotechnics - for all your Pyrotechnics supplies.
- Effects - how-to on various tricks to do with mortars.
- Pyro - Random jottings influenced by acid bath fumes, with mortar recipes
Interface
When you edit the design of a mortar, the mortar widget will appear. Through this interface you can specify how the firework behaves. A firework is comprised of 1 to 10 stages. These stages are listed in the mortar widget with the values that define their behavior.
- Add a new stage by clicking "Add Stage."
- Delete a stage (except for stage 0) by clicking that stage's "delete."
- Test fire the firework by clicking "Test Fire." You must have the necessary resources on hand, which are then loaded into the mortar. You can reclaim the resources by disarming the mortar. Test firing does not consume the resources, but only the mortar owner will see the firework.
- Scroll among the stages using the scroll bar at the bottom.
- Resize the window using the handle in the lower right.
Design
First, you'll need a mortar, which cost 10 Firebricks. The skill is learned at any University of Art & Music that has completed Pyrotechnics. Mortars are reusable; the design can always be changed and the mortar rearmed and fired. then when you click on the mortar you'll bring up 10 stages with the following options. Stage 0 is launched from the mortar; stages 1-9 are launched from another stage which you specify.
- Launch From*
- The parent of the current stage.
- Flight Time
- How long this stage will live (Max 1500.0 seconds!).
- Rockets
- The number of rockets to use per repetition. Used for rings, fans, omnis and random. (Max 4000)
- Direction
- The direction that the rocket is launched from the parent: Forward, Backward, Pitch Up, Pitch Down, Yaw Right, Yaw Left, Ring, Fan, Omni, Random.
- Launch Speed
- The speed of the rocket when it is first launched from its parent stage (Limits 0 to 6500 ft/sec).
- Launch Roll
- Rotates the rocket around its forward axis. This is a one time rotation at the moment of launch and not a rotation over time (Limits -360 deg to 360 deg).
- Thrust Forward
- The acceleration on the rocket in the forward direction (Limits -300 to 300 ft/sec2) (Note: Negative thrust can give you some strange and fun results as the speed reaches 0 and the rocket then endlessly flips over).
- Thrust Pitch Up
- The acceleration on the rocket in the vertical (z-axis) direction relative to the orientation of the rocket (Limits -300 to 300 ft/sec2).
- Thrust Yaw Right
- The acceleration on the rocket horizontal (left-right or y-axis) direction relative to the orientation of the rocket (Limits -300 to 300 ft/sec2).
- Launch Reps
- Launch another set of rockets every X seconds. Where X is total time of the parent stage divided by the number of reps. (max 250)
- Star
- The type of star to use. Only appears to lists stars that you currently have in your inventory (you must select a star type to launch or test).
Notes:
1) Egypt appears to have a gravitational acceleration of -33.00.
2) The initial stage appears to last .1 second longer than the entered time. If stage 0 is a forward launch, you can simply reduce the Flight Time to get calculated values to work (example: 0.9 sec with a 33f/s launch speed will give you a stationary platform for the next stage).
Launch Directions
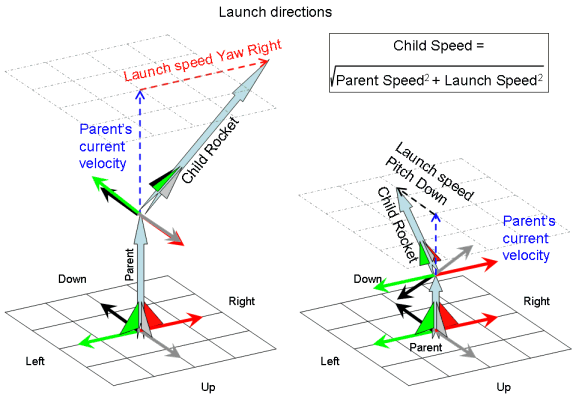
It is important to remember that child rockets will retain the movement and orientation of the parent stage at launch (Example: firing backwards from a rapidly moving rocket may well only give you a slightly slower child instead of one moving the other way). Also, now that a rocket's orientation is defined by its direction of travel, the launch directions will vary as the parent travels along its path.
- Forward sends the child in the same direction as the parent is heading.
- Backward sends the child in the opposite direction to the parent (this will either give a slower rocket moving in the same direction or one moving in the opposite direction depending on parent speed at launch and child launch speed).
- Pitch Up sends the child upwards (from the parent's point of view)
- Pitch Down sends the child down from the parent rocket (this does not necessarily mean towards the ground).
- Yaw Right sends the child to the right of the parent rocket.
- Yaw Left sends the child to the left of the parent rocket.
- Ring - child rockets fly away from the center in a ring in the plane perpendicular to the forward direction of the parent. Rockets are evenly distributed around the ring. The down direction of the children matches the backward direction of the parent.
- Fan - child rockets fly forward and away from the center in a half circle in the plane defined by the forward direction and yaw direction of the parent (need verification for all circumstances). The down direction of the children matches the down direction of the parent.
- Omni - the child rockets shoot away in a sphere.
- Random - each child is fired at a randomly chosen direction away from the parent.
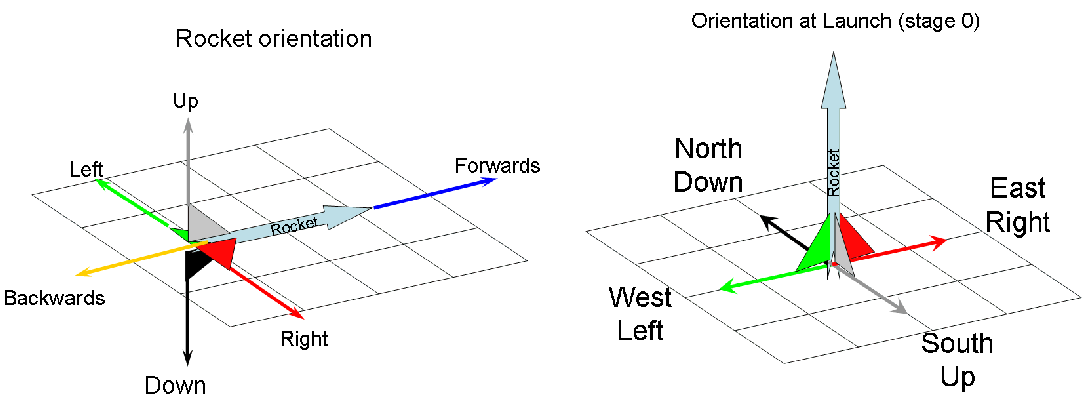
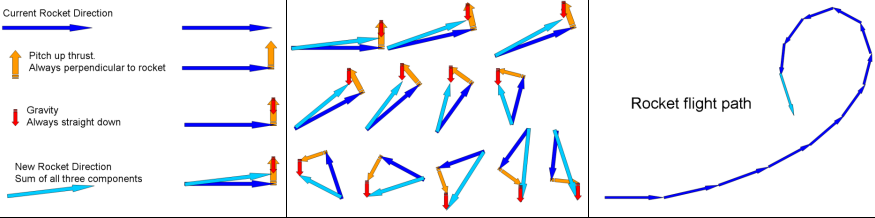
Here are some visual aides on rocket orientation and launch directions (the rocket length represents its speed)
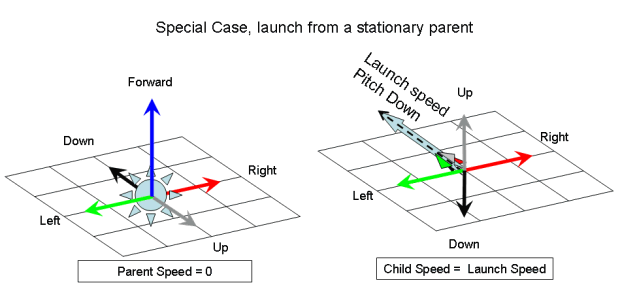
It is important to remember that if the parent star is moving when the child is launched then it will inherit its parent's speed:
While this diagram shows the parent in the most common hovering orientation (pointing straight up), it should be noted that the physics of Tale 2 pyrotechnics allow a rocket to hover in any position, however if none of the thrust are pointing straight down the necessary combination of thrusts needed to cancel out gravity can be a bit painful to calculate...
Resource costs
To arm a mortar you'll need some papyrus paper, gunpowder, and the appropriate stars. Once the mortar has been armed, it may be fired.
- Papyrus paper
- 1
- Stars
- Total # of rockets over all stages that use that type of star.
- Gunpowder
- Formula undetermined, but affected by individual stage durations, thrusts, possibly launch speeds, and of course the number of stars being moved around.
Physics
Sticking to a discussion-like style for the moment.
- Rockets no longer seem to have an orientation distinct from the direction they travel in. For example, in the following design, notice that the stage 1 rockets fire upward before stage 0's apex, and downward afterward.
| Properties | Stage 0 | Stage 1 |
| Launch From | - | 0 |
| Flight Time | 4.0 | 1.0 |
| Rockets | 1 | 1 |
| Direction | Forward | Forward |
| Launch Speed | 69.3 | 40.0 |
| Launch Roll | 0 | 0 |
| Thrust Forward | 0.0 | 0.0 |
| Thrust Pitch Up | 0.0 | 0.0 |
| Thrust Yaw Right | 0.0 | 0.0 |
| Launch Reps | 1 | 20 |
- Also, change the launch direction of stage 1 to a Pitch or Yaw direction. Notice that pitch up fires south (and pitch down fires north) before and after stage 0's apex. On the other hand, the yaw launches flip (yaw right launches east before and west after) after stage 0's apex. Thus it looks like stage 0's orientation rotates 180 degrees along the pitch axis when it reaches its apex.
- Futhermore, try launching stage 1 at pitch up; add stage 2 similar to stage 1 with but with 1 repetition; and add stage 3 identical to stage 2 but launching at pitch down and with a different star. Notice that stage 2 and 3 rockets 'flip' at stage 0's apex. This demonstrates that stage 1 has actually rotated along the pitch axis, and that launch directions do in fact appear to be relative to the rocket.
- Setting up a hovering platform:
| Properties | Stage 0 | Stage 1 |
| Launch From | - | 0 |
| Flight Time | 2.0 | 5.0 |
| Rockets | 1 | 1 |
| Direction | Forward | Forward |
| Launch Speed | 69.3 | 0.0 |
| Launch Roll | 0 | 0 |
| Thrust Forward | 0.0 | 33.00 |
| Thrust Pitch Up | 0.0 | 0.0 |
| Thrust Yaw Right | 0.0 | 0.0 |
| Launch Reps | 1 | 1 |
- Notice that the launch speed is not (gravity * flight time) as expected.
- Other hovering platform combinations:
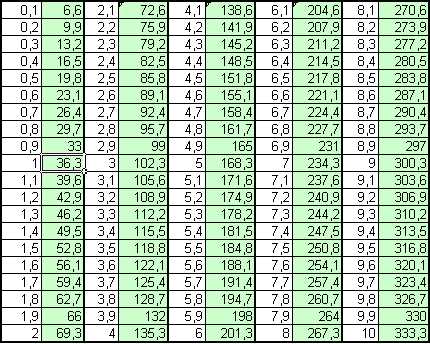
- Calculating launch speed P from flight time T: P = (33*T)+3.3 - Roen
The +3.3 for any flight time seems to come from position calculation time.
I think position is calculated every 1/10 second and, like bonfires, calculation start at time 0, not 0.1. So instead of loosing the first 3.3 ft/s at 0.1 you loose it at 0.0 That would explain the 3.3 ft/s difference between theory and observations, a 1 second flight is in fact a 1.1 seconds flight, the first 0.1 second calculated beeing at time 0.0
Roen
For a nice visual aid on Pitch, Yaw and Roll try this page : http://liftoff.msfc.nasa.gov/academy/rocket_sci/shuttle/attitude/pyr.html .
And here is a little demonstration of the effect of Pitch Up Thrust on a rocket that starts off flying horizontally, notice how the pitch causes the rocket's path to change and thus rotate it.